888888888888888888888888888888888888888888888
Mathematicians develop new theory to explain real-world randomness
888888888888888888888888888888888888888888888
Les mathématiciens développent une nouvelle théorie pour expliquer le caractère aléatoire du monde réel
par Queen Mary, Université de Londres

Crédits: CC0 Public Domain
Le mouvement brownien décrit le mouvement aléatoire des particules dans les fluides, cependant, ce modèle révolutionnaire ne fonctionne que lorsqu'un fluide est statique ou à l'équilibre.
Dans des environnements réels, les fluides contiennent souvent des particules qui se déplacent seules, comme de minuscules micro-organismes en train de nager .....Ces nageurs autopropulsés peuvent provoquer un mouvement ou une agitation dans le fluide, ce qui l'éloigne de l'équilibre.
Des expériences ont montré que les particules «passives» immobiles peuvent présenter d'étranges mouvements en boucle lorsqu'elles interagissent avec des fluides «actifs» contenant de tels nageurs. De tels mouvements ne correspondent pas aux comportements conventionnels des particules décrits par le mouvement brownien et jusqu'à présent, les scientifiques ont eu du mal à expliquer comment de tels mouvements chaotiques à grande échelle résultent en d fait d interactions microscopiques entre les particules individuelles.
Des chercheurs de l'Université Queen Mary de Londres, de l'Université de Tsukuba, de l'École Polytechnique Fédérale de Lausanne et de l'Imperial College de Londres ont présenté une nouvelle théorie pour expliquer les mouvements de particules observés dans ces environnements dynamiques.
Ils suggèrent que le nouveau modèle pourrait également aider à faire des prédictions sur les comportements de la vie réelle dans les systèmes biologiques, tels que les modèles de recherche d'algues ou de bactéries
Le Dr Adrian Baule, maître de conférences en mathématiques appliquées à l'Université Queen Mary de Londres, qui a géré le projet, a déclaré: "Le mouvement brownien est largement utilisé pour décrire la diffusion dans les sciences physiques, chimiques et biologiques; cependant, il ne peut pas être utilisé pour décrire la diffusion de particules dans des systèmes plus actifs que nous observons souvent dans la vie réelle. "
En résolvant explicitement la dynamique de diffusion entre la particule passive et les nageurs actifs dans le fluide, les chercheurs ont pu dériver un modèle efficace pour le mouvement des particules dans les fluides `` actifs '', qui tient compte de toutes les observations expérimentales.
Leur calcul approfondi révèle que la dynamique efficace des particules suit un `` vol de Lévy '', terme qui est largement utilisé pour décrire les mouvements `` extrêmes '' dans des systèmes complexes très éloignés des comportements typiques, tels que les systèmes écologiques ou la dynamique des tremblements de terre.
Le Dr Kiyoshi Kanazawa de l'Université de Tsukuba, et premier auteur de l'étude, a déclaré: "Jusqu'à présent, il n'y a eu aucune explication sur la façon dont les vols Lévy peuvent réellement se produire sur la base d'interactions microscopiques qui obéissent aux lois physiques. Nos résultats montrent que des vols Lévy peuvent survenir en raison des interactions hydrodynamiques entre les nageurs actifs et la particule passive, ce qui est très surprenant. "
L'équipe a constaté que la densité des nageurs actifs affectait également la durée du régime de vol de Lévy, suggérant que les micro-organismes nageurs pourraient exploiter les vols de nutriments de Lévy pour déterminer les meilleures stratégies de recherche de nourriture pour différents environnements.
Le Dr Baule a ajouté: «Nos résultats suggèrent que les stratégies optimales de recherche de nourriture pourraient dépendre de la densité des particules dans leur environnement. Par exemple, à des densités plus élevées, les recherches actives par le butineur pourraient être une approche plus réussie, tandis qu'à des densités plus faibles, cela pourrait être avantageux pour le butineur d' attendre simplement qu'un nutriment se rapproche alors qu'il est entraîné par les autres nageurs et explore de plus grandes régions de l'espace.
"Cependant, ce travail met non seulement en lumière la façon dont les micro-organismes nageurs interagissent avec les particules passives, comme les nutriments ou du plastique dégradé, mais révèle plus généralement comment le hasard se produit dans un environnement actif hors équilibre. Cette découverte pourrait nous aider à comprendre le comportement des autres des systèmes éloignés de l'équilibre, qui se produisent non seulement en physique et en biologie, mais aussi sur les marchés financiers par exemple. "
Le botaniste anglais Robert Brown a décrit le mouvement brownien pour la première fois en 1827, lorsqu'il a observé les mouvements aléatoires des grains de pollen lorsqu'ils étaient ajoutés à de l'eau.
Des décennies plus tard, le célèbre physicien Albert Einstein a développé le modèle mathématique pour expliquer ce comportement et, ce faisant, a prouvé l'existence d'atomes, jetant les bases d'applications généralisées en science et au-delà.
888888888888888888888888888888888888888888
Explore further
Swimming microbes steer themselves into mathematical order
More information: 'Loopy Lévy flights enhance tracer diffusion in active suspensions.' K Kanazawa, T Sano, A Cairoli, and A Baule. Nature. DOI: 10.1038/s41586-020-2086-2 , http://www.nature.com/articles/s41586-020-2086-2
Journal information: Nature
Provided by Queen Mary, University of London
88888888888888888888888888888888888888888
MES COMMENTAIRES
Cet article est plein d oublis et de références qu il convient de rappeler avant toute critique
1: Si c est bien BROWN qui la décrit le premer sur une publication , c'est en 1901, Louis Bachelier qui propose un premier modèle mathématique du mouvement brownien ;..Pal la suite beaucoup de gens trés connus ( PERRIN/LANGEVIN/EINDTEIN ) s en sont aussi occupé
2: C'est Paul Lévy qui démontre que le mouvement brownien est un cas particulier de martingale continue,...Les joueurs de casino ont détourné le sens de ce mot pour designer une methode permettant d augmenter leurs chances!!!
En fait une martingale est un type de processus stochastique (c'est-à-dire aléatoire) , tel que son espérance mathématique à l intant t dépend de l'information disponible à une certaine date .....
Ce chercheur franàais fut un des créateurs du calcul stchastique et ces " vols de LEVY "sont, par construction, des processus de Markov. Pour les distributions générales de la taille de pas, satisfaisant la condition de puissance, la distance depuis l'origine de la marche aléatoire tend, après un grand nombre de pas, à une distribution stable en raison du théorème de la limite centrale généralisée, permettant à de nombreux processus de être modélisés ..... Et comme j ai promis a certains lecteuts de les aider à mieuc comprendre , a coups de graphiques et petits dessins je vous présente quelsues uns de ces " vols"
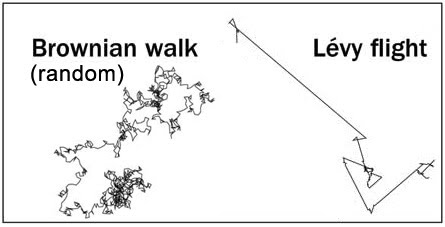
Pour revenir à l article ci dessus qui concerne plutot certaines conditions permettant à certains groupements biologiques de " s engraisser" sans trop s en faire , il faudra juger sur pieces ses exemples d utilisation
l arrivee du chinois isolè mort a PARIS est unexemple de KEVY FLIGHT ....Le deces de tous ceux qu il eu le temps de contaminer est un exemple de brownian motion ......
RépondreSupprimerOn peut voir cela comme une dualité entre l'effet de groupe (brownien) et l'aléa isolé du vol erratique (KEVY fligh).
RépondreSupprimermes yeux me jouent des tours : je parle du LEVY FLIGHT !!
RépondreSupprimer